The only way to learn MATHEMATICS
is to do MATHEMATICS.
- Paul Halmos -
3. Тригонометрийн адилтгал хувиргалт
6. Уламжлал
9. Функцийн өсөх ба буурах завсар
11. Функцийн завсар дээрх ХИ ба ХБ утга
15. Орлуулах арга
16. Хэсэгчлэх арга
18. Муруй шугаман трапецийн талбай олох
20. Шулуун ба хавтгайн харилцан байршил
21. Огтлол байгуулах
22. Цилиндр
23. Конус
24. Бөмбөрцөг
25. Призм
26. Пирамид
$\sqrt{f(x)}=g(x)\Rightarrow\begin{cases}g(x)\ge0\\f(x)=g^2(x)\end{cases}$ байх ёстой буюу манай бодлого $$\begin{cases}\sin x\ge0\\-1.5\cos x=\sin^2x\end{cases}$$ болно. Хоёр дахь тэгшитгэлийг үндсэн адилтгалаар хувиргаад бодвол $$-1.5\cos x=1-\cos^2x\Rightarrow $$$$\Rightarrow \cos^2x-1.5\cos x-1=0.$$ Энэ тэгшитгэл $\cos x=2,\ \cos x=-\dfrac12$ хялбар тэгшитгэлд шилжнэ. Мэдээж эхний тэгшитгэл шийдгүй. Иймд, бид $$\begin{cases}\sin x\ge0\\\cos x=-\dfrac12\end{cases}$$ бодлогыг бодох ёстой. Үүнийг тригонометрийн тойрог ашиглан бодвол маш хялбар бөгөөд шууд хариу нь гарна.
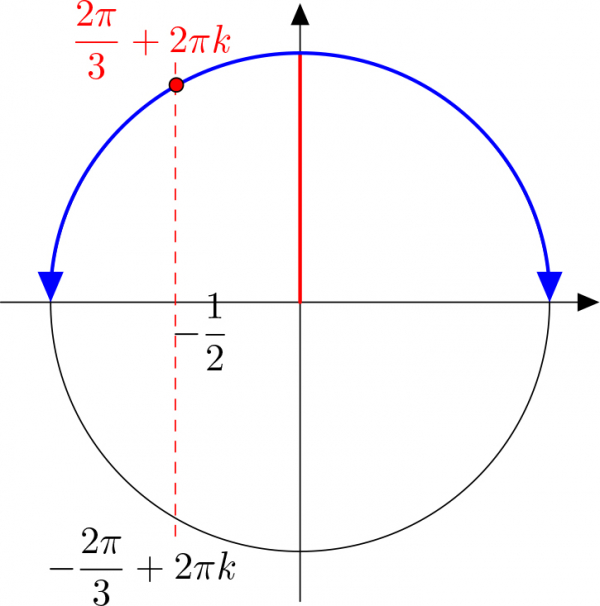
$\cos x=-\dfrac12$ байх шийдүүд $\pm\dfrac{2\pi}3+2\pi k$ боловч $\sin x\ge0$ байхын тулд тригонометрийн тойргийн дээд хагаст байгаа нь шийд болно гэсэн үг юм. Иймд зөв хариу $x=\dfrac{2\pi}3+2\pi k,\ k\in\mathbb Z$.
Төлбөр 50000₮
