Кембриджийн сургалттай сургуулиудын урьдчилсан сорил

Кембриджийн хөтөлбөртэй сургуулиудад элсэхээр бэлтгэж буй 5-р анги төгсөгчдөд зориулсан 2 сорил явуулахаар бэлтгэж байна. Эхний сорилд хүссэн үедээ ТӨЛБӨРГҮЙгээр оролцож болно. Харин дараагийн сорил 2022.06.05-ны 11.00 цагт төлбөртэйгээр (5500₮) явагдана.

СОРИЛД ОРОЛЦОХ  Эхний сорилд хүссэн үедээ оролцож болно. Хоёр дахь сорил 2022.06.05-ний 11.00 цагт эхэлж, 80 минут үргэлжлэнэ. 12.20-с өмнө хариултаа илгээсэн байх ёстой. 

12.30-д бүх сурагчийн дүн гарах бөгөөд онооны эрэмбээр жагсаж, бүртгэлийн дугаараар харагдана.

13.00 цагт сорилд оролцсон сурагчид бүх бодлогын зөв бодолт болон өөрийнхөө алдсан, оносон бодлогуудыг харж болно.

БҮРТГЭЛ Эхний сорилд оролцогч нь уг сайтад үнэ төлбөргүй бүртгүүлж, нэвтрэх эрхээ авах бөгөөд нэвтэрч орсон сурагчид хүссэн үедээ оролцох боломжтой. Нэвтрэх болон сорилд оролцох зааврыг доор оруулсан байгаа.

Харин хоёр дахь сорилд оролцох сурагчид 2022.06.04-ны 22.00 цагаас өмнө 5500₮ төгрөгийн төлбөр төлж бүртгүүлнэ.

КЕМБРИДЖ

Багцын код: tsb888

Кембриджийн сургалттай сургуулиудад элсэгчдийн багц

Төлбөр 5500

 

Авах

АНХААР

1. Сорилд оролцох төхөөрөмжийн цагийг УЛААНБААТАРын цагаар буюу UTC +8.00 гэж тааруулсан байх шаардлагатай.
2. Оролцогчийн тооноос хамааран сорил эхлэх болон дуусах мөчид ачаалал ихсэж гацах магадлалтай тул түр хүлээх, ялангуяа хариу илгээх үедээ ТАНЫ ХАРИУЛТЫГ ХҮЛЭЭН АВЛАА гэсэн бичиг гартал өөр товч дарахгүйгээр хүлээгээрэй.
3. Өмнө нь сорилд оролцож үзээгүй сурагчид энэ товч дээр дарж заавар үзээд бусад төлбөргүй сорилуудад оролцож, дадлагажаарай.

ЗӨВЛӨМЖ. Бага ангиас дунд ангид шилжих энэ эгзэгтэй үед сурагчид өгүүлбэртэй бодлогыг энгийн аргаар буюу арифметик аргаар бодож сурсан байх зайлшгүй шаардлагатай. Тэгшитгэл зохиохгүйгээр өгүүлбэртэй бодлогуудыг бодож чаддаг хүүхэд дунд, ахлах ангидаа хоцрогдолгүй суралцаж чаддаг.

Бодлого 1. $A$ хотоос $B$ хот хүрэхээр $12$км/цаг тогтмол хурдтай морьтой хүн гарчээ. $30$ минутын дараа түүнээс $4$км/цаг-аар илүү хурдтай дугуйтай хүн $B$ хотоос гарч, яг замын дунд уулзсан бол хоёр хотын хоорондох зайг ол.

Бодолт 1. $A$ хотоос $12$км/цаг тогтмол хурдтай морьтой хүн $30$ минутад $$12\mbox{км/ц}\cdot 0.5\mbox{ц}=6\mbox{км}$$ зам явна.

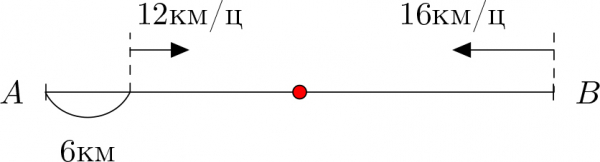
Тэр мөчөөс эхлэн $B$ хотоос дугуйтай хүн угталцах чиглэлд гарах бөгөөд дугуйтай хүн болон морьтой хүмүүсийн хурдны зөрүү $$16\mbox{км/ц}-12\mbox{км/ц}=4\mbox{км/ц}$$ юм. Мөн, тэр мөчөөс хойш явсан замын зөрүү $6\mbox{км}$ тул дугуйтай хүн гарснаас $$6\mbox{км}:4\mbox{км/ц}=1.5\mbox{ц}$$ буюу $4$ цагийн дараа уулзалдана. Өөрөөр хэлбэл, дугуйтай хүн нийтдээ $1.5$ цаг зарцуулсан гэж гарна. Иймд дугуйтай хүн нийт замын тал буюу $$16\mbox{км/ц}\cdot1.5\mbox{ц}=24\mbox{км}$$ явсан байна. Эндээс, $A,\ B$ хотуудын хоорондох зай $$24\mbox{км}\cdot2=48\mbox{км}$$ гэж олдно.