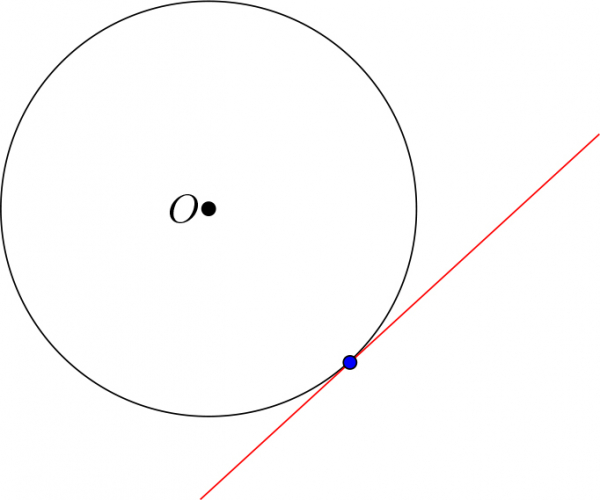
Тодорхойлолт 1. Тойрогтой ганц ерөнхий цэгтэй шулууныг шүргэгч шулуун гэдэг. Тойргийн энэ цэгийг шүргэлтийн цэг гэнэ.

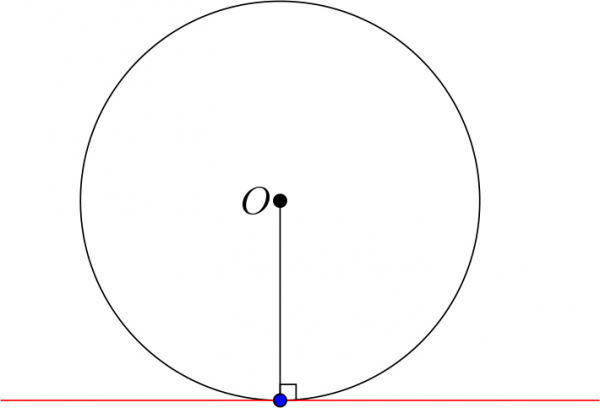
Теорем 1. Тойрогт шүргэгч шулуун шүргэлтийн цэгт татсан радиустай перпендикуляр байна.

Теорем 2. Хэрэв радиусын төгсгөлийг дайрсан шулуун энэхүү радиуст перпендикуляр байвал энэ шулуун шүргэгч болно.

Тодорхойлолт 2. Хэрэв тойрог гурвалжны тал бүрийг шүргэж байвал түүнийг багтсан тойрог гэнэ.

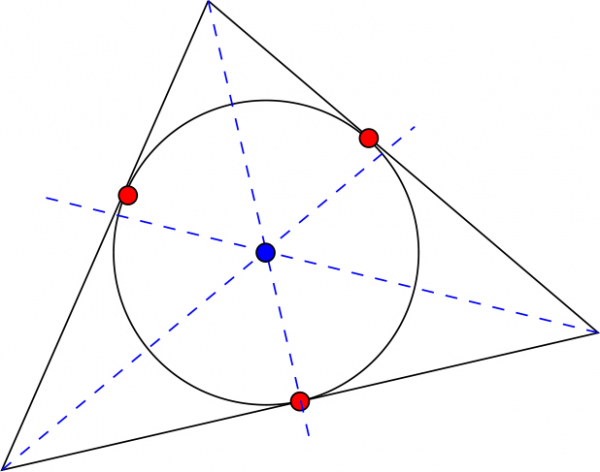
Теорем 3. Аливаа гурвалжинд тойрог багтааж болох бөгөөд тэр нь ганц байна. Уг тойргийн төв нь гурвалжны биссектрисүүдийн огтлолцлын цэг байна.

Тодорхойлолт 3. Хэрэв хоёр тойрог зөвхөн ганц ерөнхий цэгтэй бөгөөд нэг нь нөгөөгийн гадна оршиж байвал тэдгээрийг гадаад байдлаар шүргэлцсэн тойргууд гэнэ. Хэрэв хоёр тойрог зөвхөн ганц ерөнхий цэгтэй бөгөөд нэг нь нөгөөгийн дотор оршиж байвал тэдгээрийг дотоод байдлаар шүргэлцсэн тойргууд гэнэ.

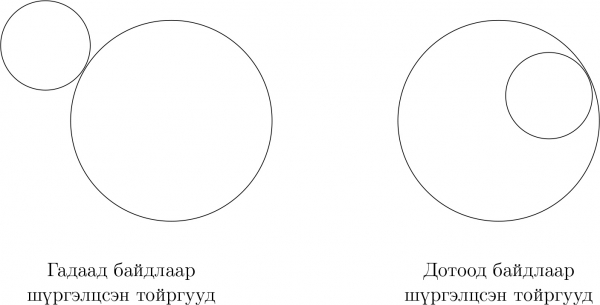
Хэрэв хоёр тойрог 2 ерөнхий цэгтэй байвал тэдгээрийг огтлолцсон тойргууд гэдэг. Хэрэв нэг ч ерөнхий цэггүй бол үл огтлолцох тойргууд гэнэ. Хэрэв тойрог дөрвөн өнцөгтийн тал бүрийг шүргэж байвал түүнийг дөрвөн өнцөгтөд багтсан тойрог, дөрвөн өнцөгтийг багтаасан дөрвөн өнцөгт}гэдэг.

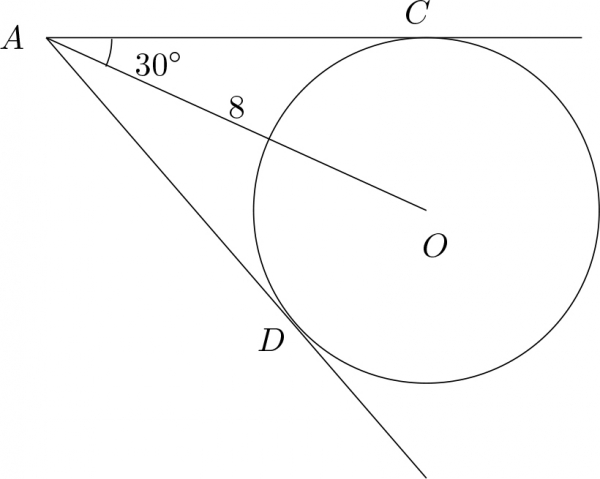
Жишээ 1. $AC$ шүргэгч бөгөөд $\angle AOC=68^\circ$ бол $\angle CAO$ өнцгийг ол.

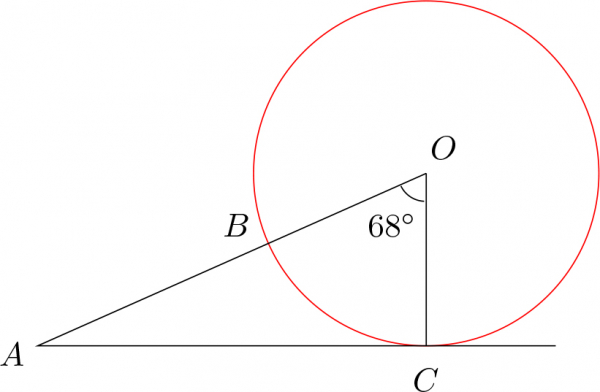
Шүргэгч нь шүргэлтийн цэгт татсан радиустай перпендикуляр байх тул $\angle OCA=90^\circ$ бөгөөд гурвалжны дотоод өнцгүүдийн нийлбэр $180^\circ$ байх тул $$\angle CAO=180^\circ-90^\circ-68^\circ=22^\circ$$ байна.

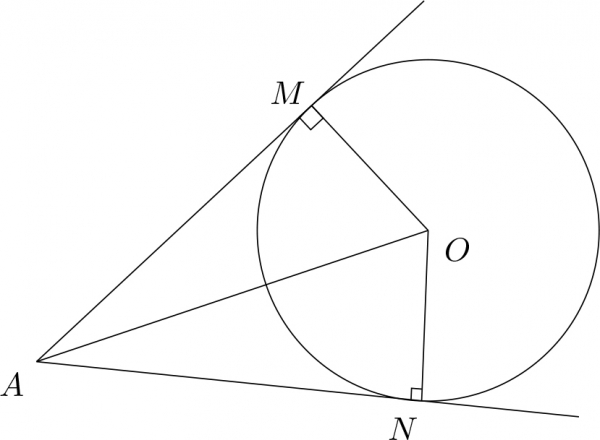
Жишээ 2. $A$ цэгээс тойрогт $AM,\ AN$ шүргэгчүүд татав. ($M,\ N$ нь шүргэлтийн цэгүүд). $AM=AN$ гэж батал.

Тойргийн төвийг $O$ гэе. Шүргэлтийн цэгт татсан радиус шүргэгчтэй перпендикуляр байх ба радиусууд тэнцүү гэдгээс $$\begin{cases}OM=PN\\ \angle AMO=\angle ANO\\AO=AO\end{cases}$$ буюу ТӨТ шинжээр $\triangle AMO,\ \triangle ANO$ гурвалжнууд тэнцүү болно. Иймд $$AM=AN$$ гэж батлагдана. Түүнээс гадна, $$\angle MAO=\angle NAO$$ болох нь батлагдах бөгөөд энэ нь өнцөгт багтсан тойргийн төв өнцгийн биссектрис дээр ордог болохыг харуулж байгаа юм.

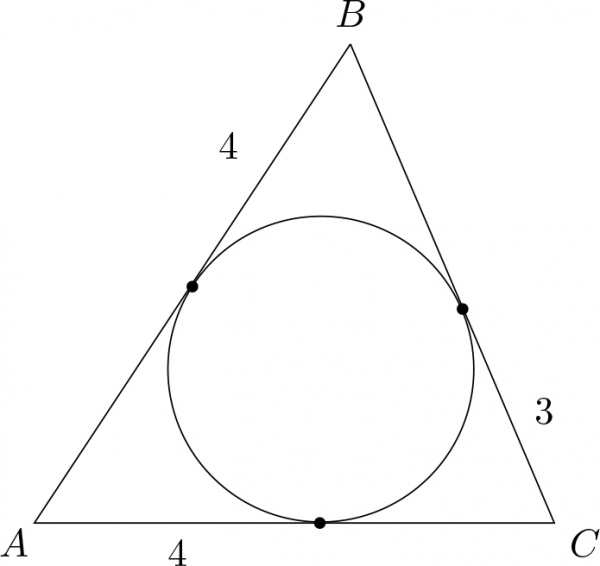
Жишээ 3. Гурвалжны периметрийг ол.

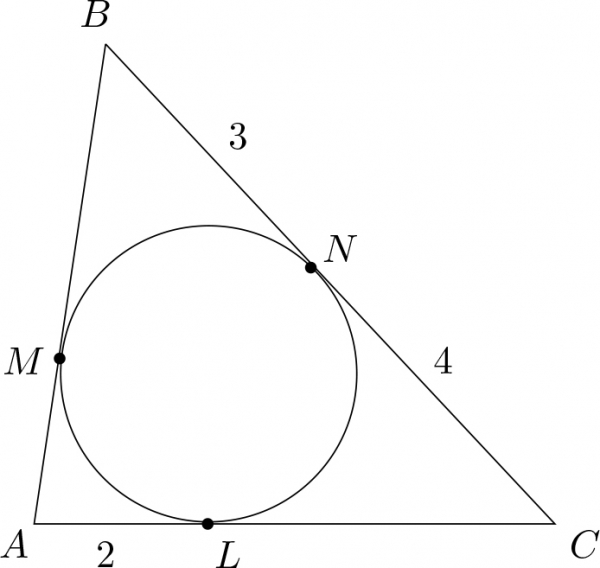
Өмнөх бодлого ёсоор нэг цэгээс татсан шүргэгчүүд тэнцүү буюу $$BM=BN=3,\ CL=CN=4,$$ $$AM=AL=2\Rightarrow$$ $$ P=\underbrace{2+3}_{AB}+\underbrace{3+4}_{BC}+\underbrace{4+2}_{CA}=18.$$

1. $ABC$ гурвалжны периметрийг ол.

   

2. Радиус нь $5$ байх тойргийн төвөөс 10 зайтай цэгээс тойрогт шүргэгчүүд татав. Шүргэгчүүдийн хоорондох өнцгийг ол.
3. $AC$ ба $AD$ нь $O$ төвтэй тойргийн шүргэгчүүд бөгөөд $AO=8$ ба $\angle CAO=30^\circ$ бол тойргийг радиусыг ол.

   

4. Тойргийн диаметрийн нэг үзүүрээс радиустай тэнцүү хөвч татав. Хоорондох өнцгийг нь ол.
5. Тойргийн $90^\circ$-н нумд тулсан хөвчийн урт $16$ бол тойргийн төвөөс энэ хөвч хүртэлх зайг ол. (Пифагорын теорем ашиглахгүй)
6. Адил хажуут тэгш өнцөгт гурвалжинд багтсан тойргийн радиус $r$ ба хагас периметр нь $p$ бол гипотенузыг ол.
7. Тойргийн ижил урттай хөвчүүд тойргийн төвөөс ижил зайд алслагдсан байна гэж батал.
8. $O$ төвтэй тойргийн $A$ цэгийг дайруулан $AB$ диаметр ба $AC$ хөвч татав. $BAC$ өнцөг $BOC$ өнцгөөс 2 дахин бага байна гэж батал.