

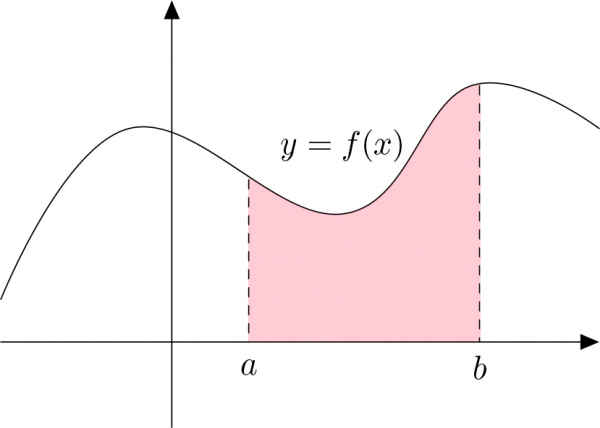
Тодорхой бус интеграл гэдэг нь уламжлалын эсрэг үйлдэл гэдгийг өмнөх хичээлээр үзсэн билээ. Тэгвэл энэ удаад $[a;b]$ завсар дээр эерэг утгатай $y=f(x)$ функц болон $Ox$ тэнхлэг, $x=a,\ x=b$ шулуунуудаар хашигдсан дүрсийг авч үзье.
Тэгвэл талбайг хэрхэн олох тухай товч тайлбарлая. Доорх зурагт $[0;x]$ завсар дахь муруй шугаман трапецийн талбайг $S(x)$, будагдсан хэсгийн талбайг $\Delta S$ гэж тэмдэглээд $\Delta S$-г тэгш өнцөгт ба гурвалжнуудын талбайн нийлбэрээр тооцож бодьё.
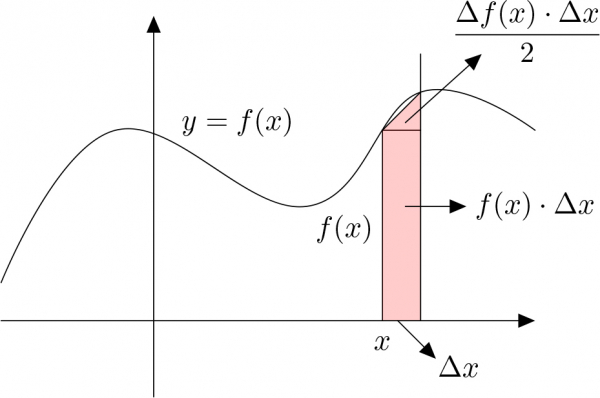
$x$ цэгийн хувь тэгш өнцөгтийн талбай $f(x)\cdot \Delta x$ байх нь ойгомжтой бөгөөд гурвалжны талбай $\dfrac{\Delta f(x)\cdot\Delta x}2$ болно. Иймд $$\Delta S=f(x)\cdot \Delta x+\dfrac{\Delta f(x)\cdot\Delta x}2\Rightarrow$$ $$\Rightarrow\dfrac{\Delta S}{\Delta x}=f(x)+\dfrac{\Delta f(x)}2$$ болно. $\Delta x\to0$ үед $\Delta f(x)\to0$ тул $$\dfrac{\Delta S}{\Delta x}=f(x)$$ болох бөгөөд эндээс $S(x)$ нь $f(x)$ функцийн эх функц байна гэсэн дүгнэлтийг хийж болно.
Тэгвэл эхний зурагт үзүүлсэн $[a;b]$ завсар дээрх муруй шугаман трапецийн талбай нь $$S_{[a;b]}=S_b-S_a$$ байх нь ойлгомжтой бөгөөд эндээс $$\int_a^bf(x)dx=F(b)-F(a)$$ гэж гарч ирнэ. Үүнийн Ньютон-Лейбницийн томьёо гэнэ. Иймд бид, тодорхой бус интегралыг сайн бодож чадвал тодорхой интеграл нь амархан гэдгийг харж авлаа. Хэрэв $y=f(x)$ функц $[a;b]$ завсар дээр сөрөг утгатай байвал түүний талбайг $$S=-\int_a^bf(x)dx\mbox{ гэж олно.}$$ Талбай олох тухай дэлгэрэнгүй хичээлийг дараагийн дугаарт оруулах болно.
Тодорхой интегралын чанарууд
$$\int_a^af(x)dx=0$$ $$\int_a^bf(x)dx=-\int_b^af(x)dx$$ $$\int_a^bf(x)dx=\int_a^cf(x)dx+\int_c^bf(x)dx$$ $$\int_a^b[f(x)+g(x)]dx=\int_a^bf(x)dx+\int_a^bg(x)dx$$ $$\int_a^bkf(x)dx=k\int_a^bf(x)dx$$
Жишээ 1. $\int\limits_0^33x^2dx$ тодорхой интегралыг бод.
$$\int_0^3 3x^2dx=3\int_0^3 x^2dx=$$$$ =3\cdot\dfrac{x^{2+1}}{2+1}\biggr\rvert_0^3=x^3\biggr\rvert_0^3=$$ $$=3^3-0^3=27.$$
Жишээ 2. $\int\limits_{1}^3\dfrac1{x^2}dx$ тодорхой интегралыг бод.
$$\int_1^3\dfrac1{x^2}dx=\int_1^3 x^{-2}dx=$$ $$=\dfrac{x^{-2+1}}{-2+1}\biggr\rvert_1^3=-\dfrac1x\biggr\rvert_1^3=$$ $$=-\dfrac13+1=\dfrac23.$$
Жишээ 3. $\int\limits_3^9\sqrt[4]{x^3}dx$ тодорхой интегралыг бод.
$$\int_3^9\sqrt[4]{x^3}dx=\int_3^9 x^{\frac34}dx=$$ $$=\dfrac{x^{\frac34+1}}{\frac34+1}\biggr\rvert_3^9=\dfrac74x^{\frac74}\biggr\rvert_3^9=$$ $$=\dfrac74\left(\sqrt[4]{9^7}-\sqrt[4]{3^7}\right).$$
Жишээ 4. $\int\limits_{-1}^4(x^2+4x+5)dx$ тодорхой интегралыг бод.
$$\int_{-1}^4(x^2+4x+5)dx=$$ $$=\int_{-1}^4 x^2dx+4\int_{-1}^4 xdx+\int_{-1}^45dx=$$ $$=\dfrac{x^3}3+4\cdot\dfrac{x^2}2+5\cdot x\biggr\rvert_{-1}^4=$$ $$=\dfrac{x^3}3+2x^2+5x\biggr\rvert_{-1}^4=$$ $$=\left(\dfrac{4^3}3+2\cdot4^2+5\cdot4\right)-$$ $$-\left(\dfrac{-1^3}3+2\cdot(-1)^2+5\cdot(-1)\right)=76\dfrac23.$$
Жишээ 5. $\int\limits_{0}^3 |x-2|dx $ тодорхой интегралыг бод.
Уг интеграл нь модуль агуулсан байгаа тул хилүүдийг салгах замаар модулиас гаргах хэрэгтэй. $|x-2|$ илэрхийлэл $$x< 2\mbox{ үед }|x-2|=2-x$$ ба $$x\ge2\mbox{ үед }|x-2|=x-2$$ тул $$\int\limits_{0}^3 |x-2|dx=$$ $$=\int\limits_{0}^2 |x-2|dx+\int\limits_2^3 |x-2|dx=$$ $$=\int\limits_{0}^2 (2-x)dx+\int\limits_2^3 (x-2)dx=$$ $$=\left(2x-\dfrac{x^2}2\right)\biggr\rvert_0^2+\left(\dfrac{x^2}2-2x\right)\biggr\rvert_2^3= 2.5$$
