Нэмэгдэж байгаа тоонуудыг ижил орны цифрүүд нь харалдаа байх (нэг багана үүсгэж байрлах)-аар бичнэ.

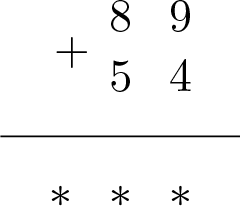
Ингэж бичих нь ижил орны цифрүүдийг хооронд нь нэмэх (орны нэмэгдэхүүний нийлбэрт задлаад ижил оронтой тоонуудыг нэг бүлэг болгож байгаатай адил юм)-ээр болгож өгч байгаа хэрэг. Ижил орны байрлалд байгаа тоонуудыг нэмэхэд тухайн “аравт хэтэрсэн” бол “хэтэрсэн тоо”-г өмнөх орон руу нь шилжүүлж түүн дээр нэмдэг.

Жишээ 1. $67+48$ нийлбэрийг баганан бичиглэлээр нэмье.

Эхлээд нэгжээр нь тэнцүүлээд баганан бичиглэлд бичвэл 

$$\begin{array}{ccc} &6&7\\ +&4&8\\ \hline \end{array}$$ болно. Нэгжүүдийг нэмбэл $7+8=15$ болох бөгөөд уг тооны нэгжийн орны цифр болох $5$-г хамгийн ард бичээд аравтын орны цифр болох $1$-г санана.

$$\begin{array}{ccc} &\stackrel{\color{red}{1}}6&7\\ +&4&8\\ \hline &&5 \end{array}$$ Одоо аравтын орнуудын цифрийг нэмвэл $6+4=10$ болох бөгөөд санасан $1$-ээр нэмбэл $11$ болно. Ингээд $$\begin{array}{ccc} &\stackrel{\color{red}{1}}6&7\\ +&4&8\\ \hline 1&1&5 \end{array}$$ болно.

Жишээ 2. $169+36$ нийлбэрийг баганан бичиглэлээр нэмье. 

Өмнөх жишээтэй ижилээр $$ \begin{array}{cccc} &\stackrel{\color{red}1}1&\stackrel{\color{red}1}6&9\\ +&&3&6\\ \hline &2&0&5 \end{array} $$

Жишээ 3. $65432+1234$ нийлбэрийг ол.

Энэ жишээний хувьд аль ч орны тоонуудыг нэмэхэд 10-аас хэтрэхгүй байгаа тул ямар нэг тоо санахгүйгээр шууд нэмнэ. $$\begin{array}{ccccccc} &6&5&4&3&2\\ +&&1&2&3&4\\ \hline &6&6&6&6&6 \end{array}$$

Жишээ 4. $40789+86021$ нийлбэрийг ол.

$$\begin{array}{ccccccc} &4&0&\stackrel{\color{red}1}7&\stackrel{\color{red}1}8&9\\ +&8&6&0&2&1\\ \hline 1&2&6&8&1&0 \end{array} $$

1. Дараах тоонуудыг баганан бичиглэлээр нэмээрэй. $$1254+8759$$ $$125483+1548$$$$100254+535800$$
2. Дутуу орхигдсон тоог олоорой. $$\begin{array}{ccccccc} &1&5&3&1&9\\ +&&2&4&4&8\\ \hline &1&7&7&*&7 \end{array}$$ $$\begin{array}{ccccccc} &3&6&3&8&5\\ +&1&5&8&4&1\\ \hline &*&2&*&*&6 \end{array}$$