Та бүртгүүлж, хэрэглэгч болоод сорилууд ажиллавал ямар бодлого дээр алдсан, ямар бодлогыг зөв бодсон болохыг харуулдаг систем ажиллана. Мөн бусад сорилуудад оролцох боломжтой болно.
1 $A(1;0)$, $B(4;4)$ цэгүүдийн хоорондох зайг ол.
2 $\dfrac{x^2+x-6}{x^2-x-2}$ илэрхийллийг хялбарчил.
3 Шулуун дээр $C,\ D,\ E$ цэгүүд энэ дарааллаараа байрлана. $CD$-ийн урт $DE$-ээс 2 дахин бага ба $CE$-ийн урт $CD$-ээс $4$ нэгжээр их бол $DE$-г ол.
4 $2,\ 8,\ 5$ гэсэн $3$ цифрийг ашиглан цифр давтагдаагүй $3$ оронтой тоо хэдийг зохиож болох вэ?
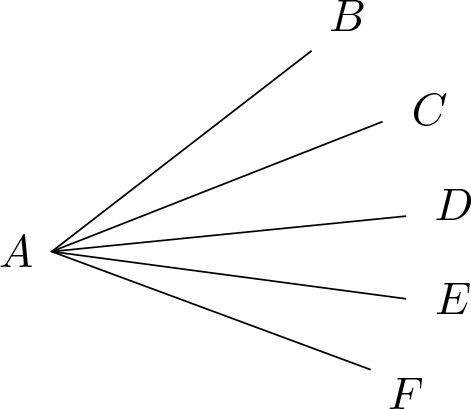
5 Зургийг ажиглаад $A$ оройтой хэдэн өнцөг байгааг тоолоорой.
6 Батад улаан ба цэнхэр өнгийн харандаа, бал нийлээд $16$ ширхэг байв. Улаан өнгийн харандаа, бал нийлээд $7$ байсан бөгөөд бал $5$ ширхэг байсны $2$ нь улаан гэж мэдэгдэж байв. Тэгвэл хэдэн цэнхэр харандаатай вэ?
7 $10-20$-н хоорондох $4$-т хуваагддаг тоонуудын олонлог ба $4-18$-н хоорондох $6$-р хуваагддаг тоонуудын олонлогуудын огтлолцол хэдэн элементтэй вэ?
8 Усан онгоц голын урсгал дагуу $180$км замыг $3$ цагт явдаг ба голын урсгалын хурд $5$км/ц бол буцахдаа хэдэн цаг зарцуулах вэ?
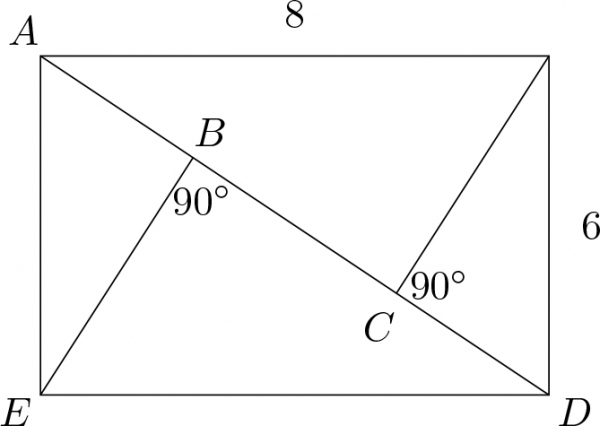
9 Дараах зургаас $AB:BD$ харьцааг олоорой.
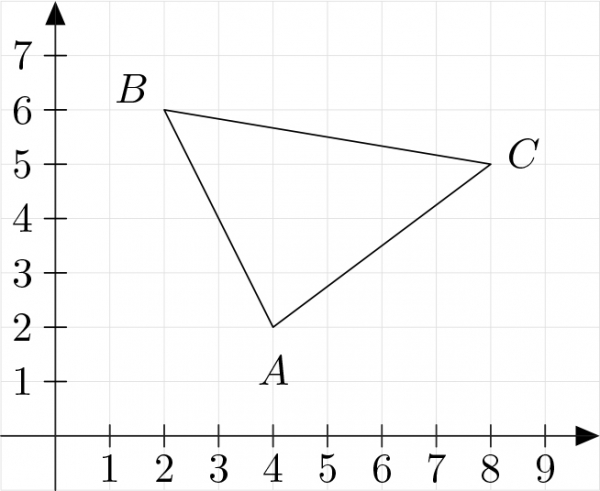
10 $ABC$ гурвалжны талбайг олоорой.
11 $\dfrac{\sqrt[4]{6-3\sqrt3}\sqrt[4]{6+3\sqrt3}}{\sqrt{\dfrac13}}$ тооцоол.
12 $f(x)=\begin{cases}x+1,x\le1\\ 3-x, x>1\end{cases}$ функц өгөгдсөн бол $f(f(2))$ утгыг ол.
13 $A=\begin{vmatrix}
2&3\\1&5
\end{vmatrix}$ ба $f(x)=x^2-2x+3$ бол $f(A)$-н утгыг ол.
14 $x\ge3\sqrt x+4$ тэнцэтгэл бишийг бод.
15 Өсөх геометр прогрессийн эхний дөрвөн гишүүний нийлбэр $120$ ба $b_1+b_3=6$ бол уг прогрессийн хуваарийг ол.
16 $y=(3x+1)^2$ функцийн графикийн $x_0=-1$ цэгт татсан шүргэгчийн тэгшитгэлийг бич.
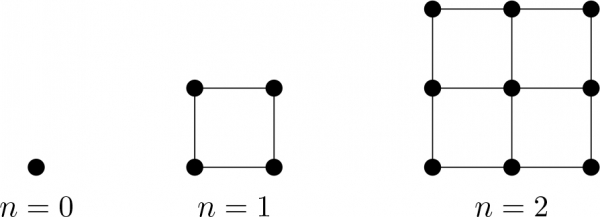
17 Дараах зурагт үзүүлснээр натурал $n$ тооны хувьд $n\times n$ хэмжээст квадратын зангилааны цэгүүдийг холбосон $1$ урттай хэрчмүүдийн тоогоор $\{a_n\}$ дараалал үүсгэе. $a_0=0$, $a_1=4$, $a_2=12$ гэх мэт үргэлжлэнэ. Тэгвэл $\{a_n\}$ дарааллын ерөнхий гишүүний томьёо аль вэ?
18 $x$-ээс хамаарсан $y$ функц нь $$\begin{cases}y=t^2+3t+1\\ x=2t+1\end{cases}$$ параметрт тэгшитгэлээр тодорхойлогдсон байв. Уг функцийн графикийн дурын цэгт татсан шүргэгч шулууны налалтыг $t$-ээр илэрхийлж ол.
19 $3\mbox{tg}\dfrac{107\pi}6+4\sin\dfrac{37\pi}3$ илэрхийллийн утга.
20 $\log_{\sqrt2}2$ илэрхийллийн утгыг ол.
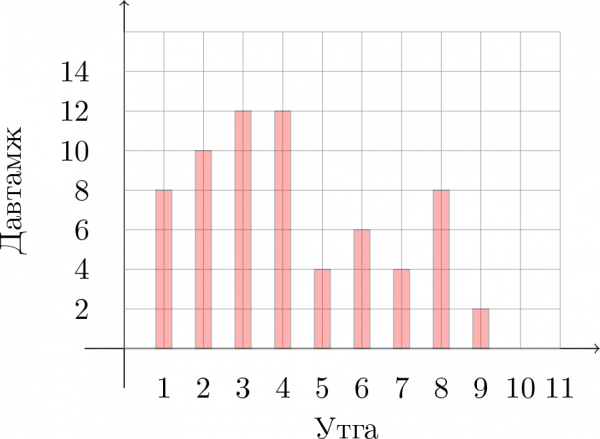
1 Дараах диаграммаар өгөгдсөн өгөгдлийн далайц $\fbox{a}$, дундаж $\approx\fbox{b.cd}$, медиан $\fbox{e}$ байна.
2 $f(x)=x\cdot e^{-3x}$ функцийн хувьд $$f_{\max}=f\left(\dfrac{\fbox a}{\fbox b}\right)=\dfrac1{\fbox c\cdot e}$$ байна. Энд $(\fbox a;\fbox b)=1$.
3 Дараалсан сондгой тоонуудын квадратуудын нийлбэр $970$ гэж өгчээ. Эхний тоог $k$ гэвэл дараагийн тоо $k+\fbox a$ бөгөөд эдгээрийн квадратуудын нийлбэр $$\fbox b k^2+\fbox c k+\fbox d$$ болно. Үүнийг $970$-тай тэнцүүлээд бодвол $k=\fbox{ef}$ гэж гарна.
4 $z_1=2-2i$, $z_2=\sqrt3+i$, $z_3=a+bi,\ a,b\in\mathbb R$ тоонууд өгөгдөв.
а) Хэрэв $|z_1z_3|=16$ бол $$|z_3|=\fbox a\sqrt{\fbox b}\mbox{ байна.}$$
б) $\arg\left(\dfrac{z_3}{z_2}\right)=\dfrac{7\pi}{12}$ бол $$\arg z_3=\dfrac{\fbox c\pi}{\fbox d}$$
в) $\dfrac{z_3}{z_1}=-2$ бол $a=-\fbox e$, $b=\fbox f$ байна.

